Espaço e Forma
Em construção... aguarde.
Noções de Geometria
A Geometria é o ramo da matemática que estuda as formas, tamanhos e posições das figuras no espaço. Seus conceitos fundamentais, como ponto, reta e plano, são a base para construir polígonos, círculos e sólidos complexos. Essencial desde a antiguidade, seus princípios são aplicados na arquitetura, engenharia, arte e na compreensão das estruturas do nosso universo.
Atividade:
Ângulos
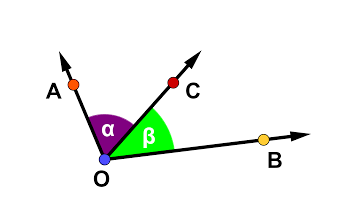
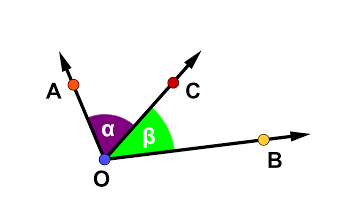
Um ângulo mede a rotação ou a abertura entre duas retas que se encontram em um ponto comum, o vértice. Essa medida, expressa em graus (∘), é o que define a forma de todas as figuras geométricas e a inclinação de qualquer superfície. O entendimento de ângulos retos, agudos e obtusos é a base para a construção civil, o design e até a astronomia.
Atividade:
Polígonos
Polígonos são figuras geométricas planas e fechadas, formadas por segmentos de reta que se encontram nos vértices. São classificados pelo número de lados. Quando possuem todos os lados e ângulos iguais, são chamados de regulares, representando a simetria e a base para a criação de mosaicos e estruturas complexas.
Atividade:
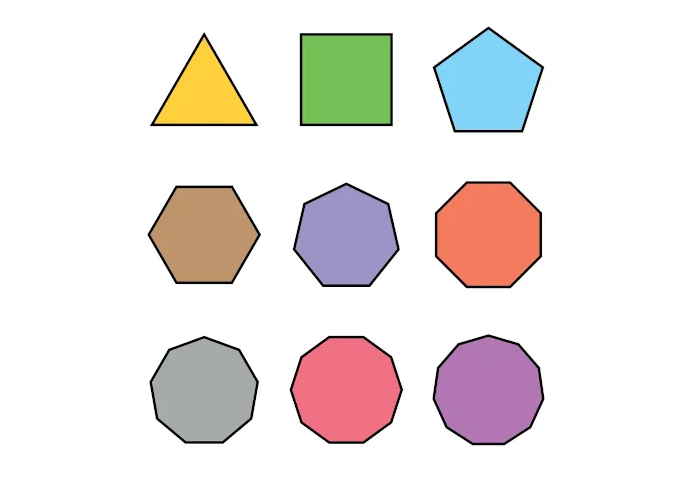
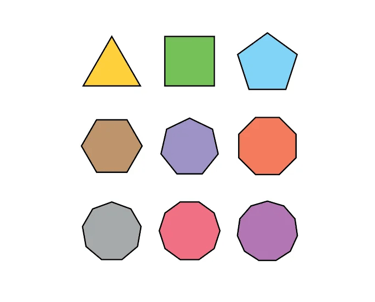
Circunferência
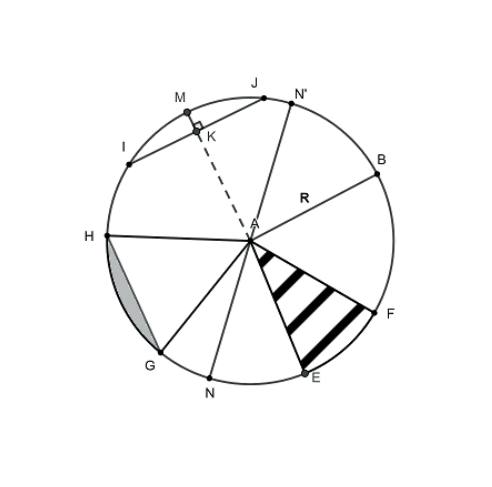
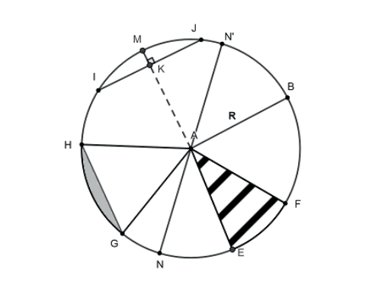
Circunferência é o conjunto de todos os pontos de um plano que estão a uma mesma distância, chamada raio, de um ponto fixo, o centro. É a linha que define o contorno do círculo. Essencial em geometria, seu comprimento é determinado pela famosa constante π (Pi), e suas propriedades são fundamentais para a criação de rodas, engrenagens e no estudo das órbitas planetárias.
Atividade:
Triângulos e Quadriláteros
Triângulos e quadriláteros são os polígonos mais fundamentais. O triângulo, com seus três lados, é a base da rigidez estrutural na engenharia e se classifica por lados ou ângulos. Já os quadriláteros, figuras de quatro lados, formam um grupo diverso que inclui quadrados, retângulos e losangos, cada um com propriedades únicas que definem os espaços e objetos do nosso cotidiano.
Atividade:
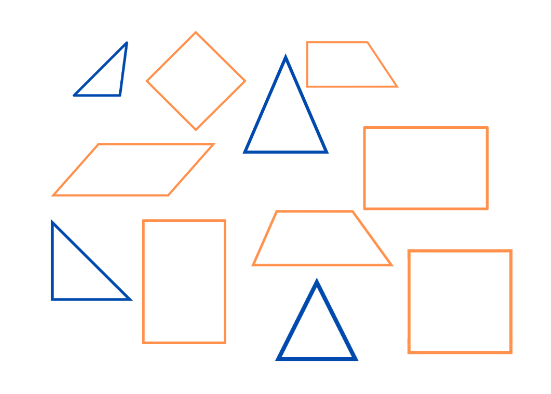
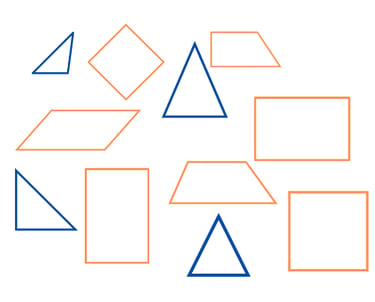
Semelhança entre figuras
A semelhança descreve figuras que possuem a mesma forma, mas não necessariamente o mesmo tamanho. Para que duas figuras sejam semelhantes, seus ângulos correspondentes devem ser iguais e seus lados correspondentes, proporcionais. Esse princípio é a base de mapas, maquetes e do zoom em fotografias, permitindo ampliar ou reduzir objetos sem distorcer suas características essenciais.
Atividade:
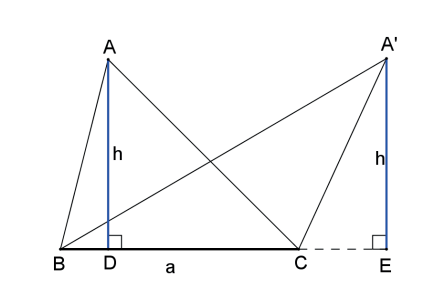
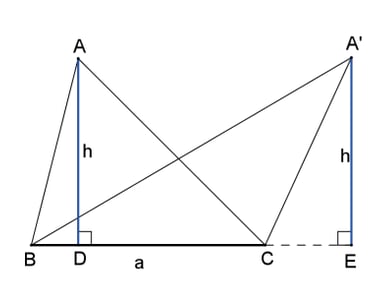
Área e Perímetro
Área e perímetro são duas medidas fundamentais de figuras planas, mas com significados distintos. Perímetro é o comprimento do contorno da figura, a soma de todos os seus lados, medindo a sua borda. Já a área é a medida da superfície interna, o espaço que a figura ocupa. Entender ambos é crucial para projetos, desde calcular a cerca de um terreno (perímetro) até o piso para cobri-lo (área).
Atividade:
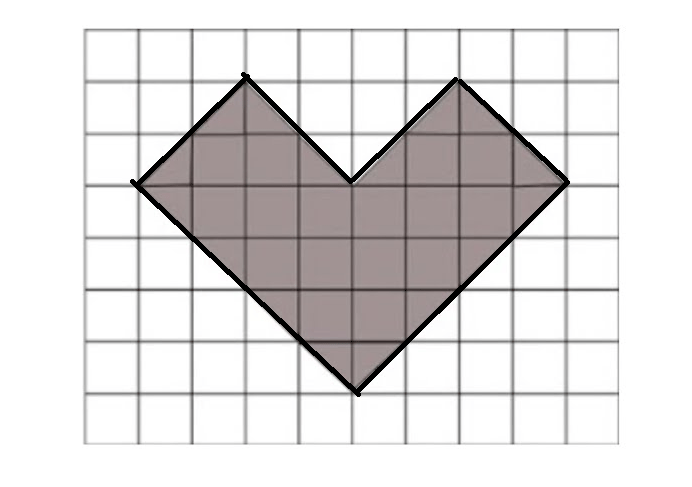
Teorema de Pitágoras
O Teorema de Pitágoras é uma das relações mais célebres da matemática, aplicável a qualquer triângulo retângulo. Ele afirma que o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos catetos. Representado pela fórmula h² = a² + b², é uma ferramenta essencial para calcular distâncias, sendo fundamental na arquitetura, engenharia e navegação.
Atividade:
Razões Trigonométricas
As razões trigonométricas – seno, cosseno e tangente – são relações fundamentais entre os ângulos e os lados de um triângulo retângulo. Elas permitem calcular distâncias e ângulos inacessíveis, conectando a geometria com a álgebra. Essas ferramentas são a base para a navegação, astronomia, engenharia e física, sendo essenciais para descrever fenômenos ondulatórios como o som e a luz.
Atividade:
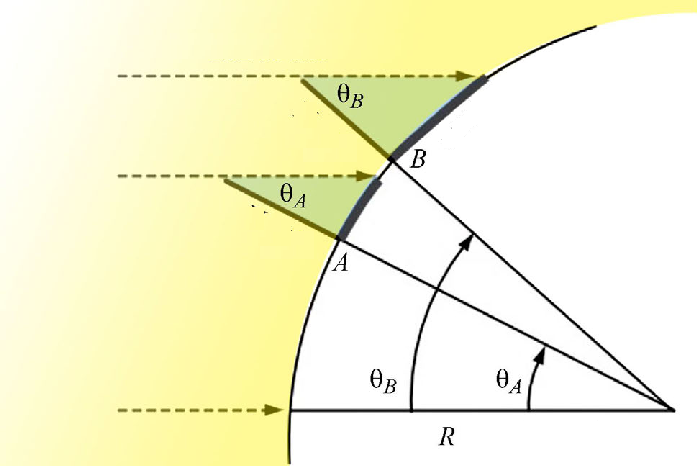
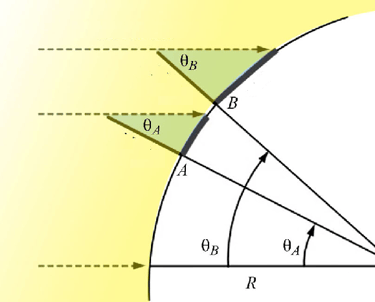
Transformações Geométricas
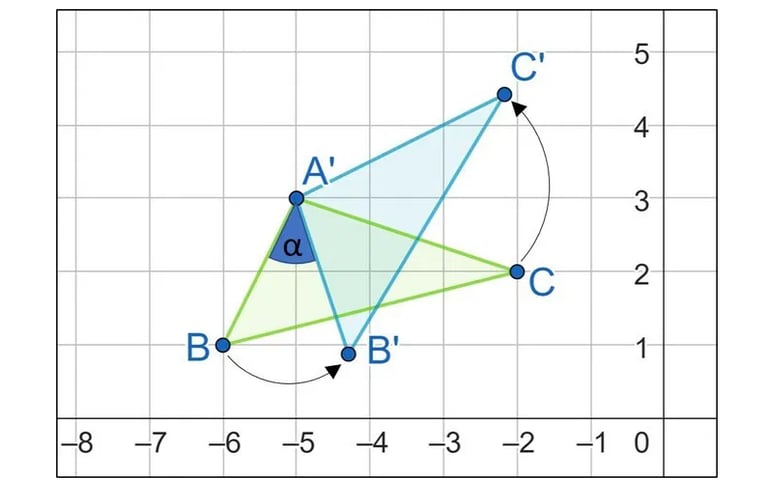
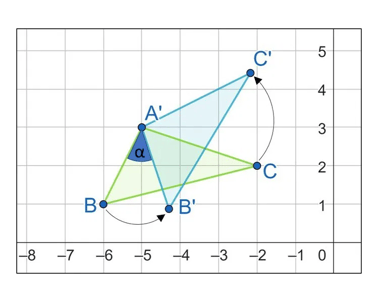
Transformações geométricas são processos que alteram a posição, orientação ou tamanho de uma figura no plano sem modificar sua forma. As principais são a translação (deslocar), a rotação (girar) e a reflexão (espelhar). Elas são a base matemática por trás da simetria na natureza, da arte, das animações por computador e do design, descrevendo como os objetos se movem e se relacionam no espaço.
Atividade:
Poliedros
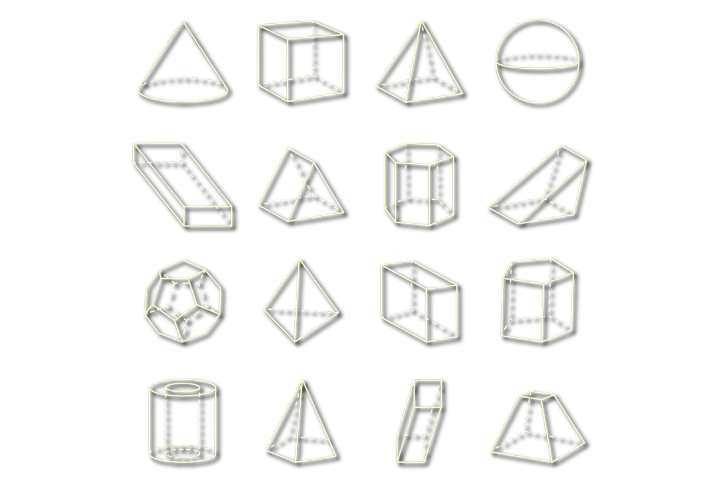
Poliedros são sólidos geométricos tridimensionais cujas superfícies são compostas por polígonos planos, chamados faces. Seus elementos principais incluem as faces, as arestas (encontro de duas faces) e os vértices (encontro de arestas). Exemplos clássicos como cubos, pirâmides e os elegantes Sólidos Platônicos formam a base da geometria espacial e da cristalografia.
Atividade:
Volume
Volume é a medida do espaço tridimensional ocupado por um corpo ou a capacidade que um recipiente possui. Enquanto a área mede uma superfície (2D), o volume quantifica o espaço interior de um sólido (3D), sendo geralmente expresso em unidades cúbicas, como o metro cúbico (m³). Seu cálculo é essencial para a engenharia, química e para atividades cotidianas, como encher uma piscina.
Atividade:
"A educação não transforma o mundo. A educação muda as pessoas. Pessoas transformam o mundo."
Paulo Freire
